 В школе все мы изучали алгебру, только про булеву алгебру там не говорили. Чем отличается булева алгебра от школьной, история ее появления, задачи и области применения описаны в данной статье.
В школе все мы изучали алгебру, только про булеву алгебру там не говорили. Чем отличается булева алгебра от школьной, история ее появления, задачи и области применения описаны в данной статье.
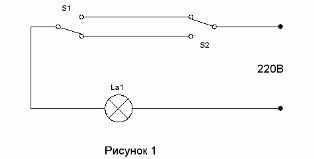
Схема, позволяющая двумя выключателями лампочку в коридоре включить при входе в коридор и выключить, войдя в комнату известна очень давно (cм. Коридорная схема управления освещением). Она показана на рисунке 1.
Задача №1. Более сложная. Составить схему, позволяющую включать и выключать свет в вашей комнате любым из 3 различных выключателей. Выключатели расположены у входа в комнату, над постелью и у письменного стола.
Задача № 2.
В спортивном комитете, например заводском, собралось 5 судей.
Каждый из них должен голосовать за принятие различных решений. Решение принимается большинством голосов, но только при том дополнительном условии, что за него голосует председатель комитета.
Судьи голосуют путем нажатия кнопки, замыкающей переключатель, расположенный под столом, за которым они сидят. Замыкая переключатель, они голосуют «за», размыкая «против». Начертите простейшую схему, позволяющую автоматически видеть результаты голосования. В простейшем случае просто с помощью лампочки, - зажглась – решение принято, не зажглась,- нет.
Задача №3. Практически такое маловероятно, но в качестве сложной учебной задачи вполне подойдет.
В большой шестиугольной комнате на каждой стене установлено по одному переключателю. Постройте такую схему, чтобы в любой момент можно было включать или выключать свет в комнате поворотом одного (любого) переключателя.
После того, как вы безрезультатно просидите над задачами три-четыре дня, отложите их временно в сторону. И займитесь алгеброй Буля. Именно алгебра Буля, или, как ее еще называют, булева алгебра, алгебра релейных схем, поможет вам решить составленные задачи.
Что же такое алгебра Буля?
Как ни странно, несмотря на то, что пять лет в школе изучают алгебру, многие ученики, а впоследствии и взрослые, не смогут ответить на вопрос, а что такое алгебра? Алгебра — это наука, которая изучает множества некоторых элементов и действия над ними.
В школьном курсе алгебры такими элементами являются числа. Числа можно обозначать не цифрами, а буквами, с этим все знакомы. На первых уроках алгебры это всегда затрудняет многих учеников. Вспомните, как трудно было вначале привыкнуть вместо цифр складывать буквы, решая ничего не говорящие уравнения.
Наверное, каждый из нас тогда задавал себе вопрос: «Для чего нужно вводить буквы вместо цифр и, нужно ли это вообще?». И только позднее вы убедились, какие преимущества при решении задач дает алгебра в сравнении с арифметикой.
Алгебра применяется во многих точных науках. Это физика, механика, сопромат, электричество. Закон Ома есть не что иное, как алгебраическое уравнение: достаточно вместо букв подставить их числовые значения, чтобы узнать какой ток будет протекать в нагрузке, или какое сопротивление имеет участок цепи.
Так вы познакомились с алгеброй чисел, или с элементарной алгеброй. Основная и почти единственная задача — получить ответ на вопрос: «Чему равняется X? Сколько?»
В старших классах школы изучают начала векторной алгебры. Эта алгебра принципиально отличается от элементарной алгебры. В ней совершено другая природа изучаемого множества и другие правила действий. Решая векторное уравнение, получаем в ответе вектор, который не является обычным числом, отвечающим на вопрос «Сколько?»
Формулы векторной алгебры во многом отличны от формул элементарной алгебры. Например, и в элементарной алгебре и в векторной имеется операция сложения. Но выполняется она совершенно по-разному. Сложение чисел выполняется совсем не так, как сложение векторов.
Существуют и другие алгебры: линейная алгебра, алгебра структур, алгебра колец, алгебра логики, или, что то же самое, алгебра Буля. На школьных уроках вы, наверное, не слышали имени Джорджа Буля — зато всем известно имя одной из его талантливых дочерей Этель Войнич (1864 – 1960). Она написала роман «Овод», где рассказывается о борьбе за свои права итальянских карбонариев.
 Джордж Буль родился в Англии 2 ноября 1815 года. Всю свою жизнь он работал учителем математики и физики в школе. Из воспоминаний его учеников известно, какое огромное значение придавал Буль развитию творческих способностей учащихся. При изложении нового материала он стремился к тому, чтобы его ученики сами заново «открывали» некоторые формулы и законы.
Джордж Буль родился в Англии 2 ноября 1815 года. Всю свою жизнь он работал учителем математики и физики в школе. Из воспоминаний его учеников известно, какое огромное значение придавал Буль развитию творческих способностей учащихся. При изложении нового материала он стремился к тому, чтобы его ученики сами заново «открывали» некоторые формулы и законы.
Рассказывая ученикам о трудностях, с которыми ученые неизбежно сталкивались в поиске истины, учитель любил повторять одну восточную мудрость: даже персидский трон не может принести человеку столько наслаждений, как самое маленькое научное открытие. Буль никогда не терял надежды, что когда-нибудь и его ученики сделают настоящее открытие.
Диапазон научных интересов Буля был очень широк: в равной степени его интересовали математика и логика — наука о законах и формах мышления. В те времена логика считалась гуманитарной наукой, и многих, кто знал Джорджа Буля, удивляло, как в одном человеке могли уживаться точные методы познания, присущие математике, и чисто описательные методы логики.
Но ученому захотелось сделать науку о законах и формах мышления такой же строгой, как и любая из естественных наук, скажем математика и физика. Для этого Буль стал обозначать буквами не числа, как это делается в обычной алгебре, а высказывания и показал, что такими уравнениями, очень схожими с алгебраическими, можно решать вопросы об истинности и ложности высказываний, сделанных человеком. Так возникла алгебра Буля.
Но еще задолго до Джорджа Буля немецкий математик и философ Готфрид Лейбниц (1646—1716) впервые высказал идею о создании науки, которая обозначит все понятия обычной разговорной речи символами и установит некоторую новую алгебру для соединения этих символов.
После создания такой науки, по мнению Лейбница, ученые и философы перестанут спорить и перекрикивать друг друга, выясняя истину, а возьмут в руки карандаш и спокойно скажут: «Давайте-ка вычислять!»
 В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.
В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.
Новым в алгебре Буля является то, что элементы множества, которые в ней изучаются, являются не числами, а высказываниями. Если при решении обычных алгебраических уравнений определяется, какому числу равняется неизвестное X, школьная алгебра ищет ответ на вопрос: «Сколько?»
Алгебра логики ищет ответ на вопрос: «Верно ли то или другое высказывание, обозначенное буквой X?»
Смысл и содержание высказывания здесь не играют никакой роли. Каждое высказывание может быть только или истинным, или ложным. Оно не может быть наполовину истинным и наполовину ложным. В качестве примера можно вспомнить метание жребия при помощи монеты.
Там рассматриваются только два состояния монеты — орел или решка. По договоренности сторон орел это ДА, а решка это НЕТ. Никакие другие промежуточные положения в теории вероятностей не учитываются, хотя они и возможны. Подброшенная монета может упасть на ребро, докатиться по полу до ножки стула или стола и так и остаться в вертикальном положении, а то и вообще провалиться в широкую щель в полу. (По аналогии с электрическими схемами две последних ситуации можно рассматривать как неисправность в виде обгоревшего контакта). Но в те далекие времена булева алгебра, увы, широкого распространения не получила.
 Вновь «открыл» алгебру Буля Клод Шеннон. В 1938 году, будучи еще студентом Массачусетского технологического института и Америке, молодой Клод доказал, что алгебра Буля полностью подходит для анализа и синтеза релейных и переключательных схем.
Вновь «открыл» алгебру Буля Клод Шеннон. В 1938 году, будучи еще студентом Массачусетского технологического института и Америке, молодой Клод доказал, что алгебра Буля полностью подходит для анализа и синтеза релейных и переключательных схем.
С помощью алгебры Буля можно очень просто составить электрическую схему автомата, работающего на реле. Для этого, оказывается, нужно только точно знать, что должен делать автомат, то есть нужно иметь алгоритм его работы. Так была заложена основа теории цифровых машин, действующих по принципу ДА или НЕТ.
Такова вкратце история булевой алгебры. В следующих статьях мы рассмотрим ее основные законы, примеры контактных схем реализующие эти законы. Рассмотрим решение тех задач, которые были приведены в начале статьи.
Продолжение статьи: Булева алгебра. Часть 2. Основные законы и функции
Борис Аладышкин



 В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.
В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.
